三角形數

三角形數

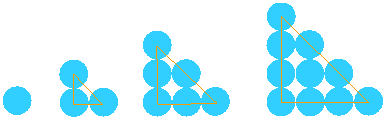1、3、6、10、15、21、28 .....是一列三角數，如果以Tn表示第n個三角數， 則Tn = n(n+1)/2。

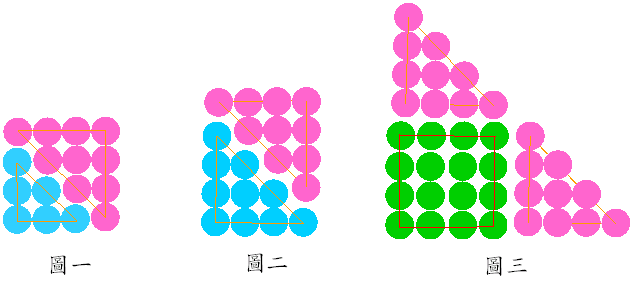
(圖一) 是T3 + T4 =  42 的圖示，如果推廣之，可得   Tn-1+ Tn =  n2 。 這是因為 Tn-1+ Tn =  (n-1)(n-1+1)/2+n(n+1)/2=n(n-1+n+1)/2 = 2n2/2  = n2 。 (圖二) 是 2T4 = 4 × 5的圖示，如果推廣之，可得2Tn = n(n+1)。 這是因為2Tn=2n(n+1)/2 = n(n+1)。 (圖三) 是 T2×4=2T4+42的圖示，如果推廣之，可得T2×n=2Tn+n2。這是因為 T2×n=(2n)(2n+1)/2 = n(2n+1)=2n2+n = n2+n+n2 = [2(n2+n)/2]+n2 =2Tn+n2。

(圖四) 是 T2×4+1=3T4+T5的圖示，如果推廣之，可得T2n+1=3Tn+Tn+1。這是因為 T2n+1=(2n+1)(2n+2)/2 = (2n+1)(n+1)；而且3Tn+Tn+1= 3[n(n+1)/2]+[(n+1)(n+2)/2] = (n+1)[(3n+n+2)/2] = (2n+1)(n+1)。 同學可以試試說明以下關係式： 1.   Tm+n = Tm + Tn + m×n 2.   如果 n > m ，則 Tm + Tn = Tn-m + m×(n+1)