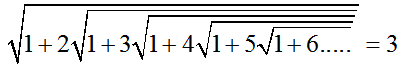
若函數f(x)=x(x+2),其中x是正整數,則f(x+1)=(x+1)(x+3)=(x+2)2-1,因此1+f(x+1)=(x+2)2,x+2=1+f(x+1)−−−−−−−−−−√ ,所以f(x)=x1+f(x+1)−−−−−−−−−−√ 。
使用函數f(x)=x1+f(x+1)−−−−−−−−−−√ 迭代計算可得f(x+1)=(x+1)1+f(x+2)−−−−−−−−−−√ ,因此f(x)=x1+(x+1)1+f(x+2)−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−√ 。
因為f(x+2)=(x+2)1+f(x+3)−−−−−−−−−−√ ,所以
f(x)=x1+(x+1)1+(x+2)1+f(x+3)−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√ 。
因為f(x+3)=(x+3)1+f(x+4)−−−−−−−−−−√ ,所以
f(x)=x1+(x+1)1+(x+2)1+(x+3)1+f(x+4)−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√ 。
如此迭代計算下去,可得
f(x)=x1+(x+1)1+(x+2)1+(x+3)1+(x+4)...1+(x+n−1)1+f(x+n)−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−⎷−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−⎷−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−⎷ ,其中n是趨向無限大的正整數。
當上列恆等式中的x=1時,f(1)=1×3=3
3=f(1)=1×1+f(2)−−−−−−−√ =1×1+2×4−−−−−−−√
3=f(1)=1×1+21+f(3)−−−−−−−√−−−−−−−−−−−−−√ =1×1+21+3×5−−−−−−−√−−−−−−−−−−−−−√
3=f(1)=1×1+21+31+f(4)−−−−−−−√−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−√ =1×1+21+31+4×6−−−−−−−√−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−√
3=f(1)=1×1+21+31+41+f(5)−−−−−−−√−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−√ =1×1+21+31+41+5×7−−−−−−−√−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−√−−−−−−−−−−−−−−−−−−−−−−−−−√
....................
20世紀印度數學英才拉馬努金(Ramanujan),擁有非常人的數感,具有前瞻性的洞察力,在其數學成就中就包含約4000個恆等式,但是有一些恆等式雖有結論,卻沒有留下詳細的推論過程。
本文的恆等式就是由拉馬努金(Ramanujan)所提出的。
3=f(1)=
....................
20世紀印度數學英才拉馬努金(Ramanujan),擁有非常人的數感,具有前瞻性的洞察力,在其數學成就中就包含約4000個恆等式,但是有一些恆等式雖有結論,卻沒有留下詳細的推論過程。
本文的恆等式就是由拉馬努金(Ramanujan)所提出的。

沒有留言:
張貼留言