三等份圓面積

三等分圓面積

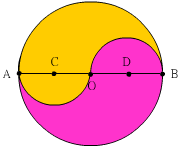二等分圓周與二等分圓面積只要直徑(AB)就可以完成，也可以如太極圖一般(如左圖)，左圖中AB是圓O的直徑，C點和D點是半徑AO、半徑BO的中點，以直徑AO、直徑BO作半圓。

如果要三等分圓周，只要作圓內接正三角形，此正三角形的三個頂點就可以三等分圓周。那麼要如何三等分圓面積呢？

如果圓的半徑是r，三等分此圓面積得每一等分面積是⅓ πr²。想一想，若以原來的圓心作小圓的圓心，而小圓半徑取⅓r² 的正平方根，則小圓面積就是原來圓面積的⅓。其他的區域是點對稱的圓環，因為此圓環的面積占原來圓面積的⅔，若將它二等分則每等分各占原來圓面積的⅓。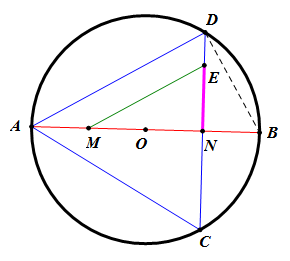

我們先談如何三等分圓周，如右圖在圓O直徑AB上取AO的中點M和BO的中點N，過N點作中垂線交圓O於C點和D點。
右圖中，△OBD是正三角形，因此∠ABD=60∘，又因為∠ADB=90∘，所以∠DAB=30∘。
同理，∠CAB=30∘。因為∠DAC=∠DAB+∠CAB，所以∠DAC=60∘。
圓O中，∠C和∠ABD都對弧AD，因此∠C=∠ABD=60∘，由以上說明可知△ACD是等角的正三角形，因此頂點A、C、D三等分圓周。
現在再談如何三等分圓O面積，假設圓O半徑長 r，如右上圖，作 ME / / AD，ME交CD於E點。因為 ME / / AD， MN：NA=2：3，所以 NE：ND=2：3。
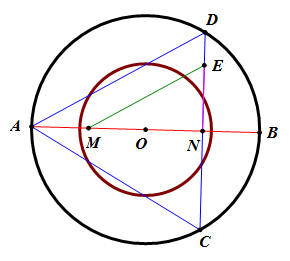
直角△ABD中，∠ADB=90∘，DN⊥AB，由直角△母子相似性質可知 DN²=AN×NB，因此DN²= [(½)r×3] ×(½) r = (¾ ) r²，DN=(^√3/₂) r 。因為 NE：ND=2：3，NE=(⅔)ND，所以NE=(⅔)(^√3/₂) r =(^√3/₃₎ r。如圖一，以O點作圓心，半徑長 (^√3/₃₎ r ，則圖一的小圓O面積就是⅓πr²。圖一的圓環面積是 πr² − ⅓ πr² =(⅔)πr²。
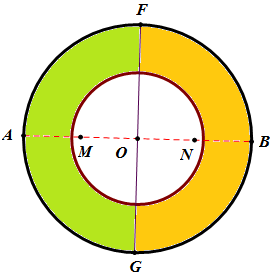
再作圓O直徑AB的中垂線交圓O於F點和G點，則FG二等分圓環(如圖二)，兩區域(綠色和黃色)的面積都是⅓ πr²。
綜合上述說明，可知圓O的面積被三等分，如圖二所示，綠色、黃色區域和小圓O的面積相等。