
上回我們分析內外圈跑道的差距,知道賽跑時,每圈的起點都要往前挪動「跑道寬度×6.28」的距離,各跑道的賽跑距離才相等。不過,像大隊接力或800公尺這種得跑好幾圈的比賽,到第二圈時,外圈跑者勢必要往內圈切,不然就會被隊友跟教練罵死
「有這麼喜歡多跑嗎!?」
問題來了。請問外圈跑者在跑第二圈時,該採取怎樣的「切內圈」策略呢?
§
位在第N條跑道的跑者跟內圈的距離是(N-1)×跑道寬度。假如是第4條跑道的跑者,以上週的數據跑道寬度1.2公尺來說,這段距離是3.6公尺。如果跑者採取一進入第二圈就立刻轉90度直奔內圈,他得多跑上3.6公尺。聽起來有點笨,一般人決計不會這樣跑。可是,一定也不是每個人都會想到最佳的切內圈策略。這個策略跟直角三角形有關。
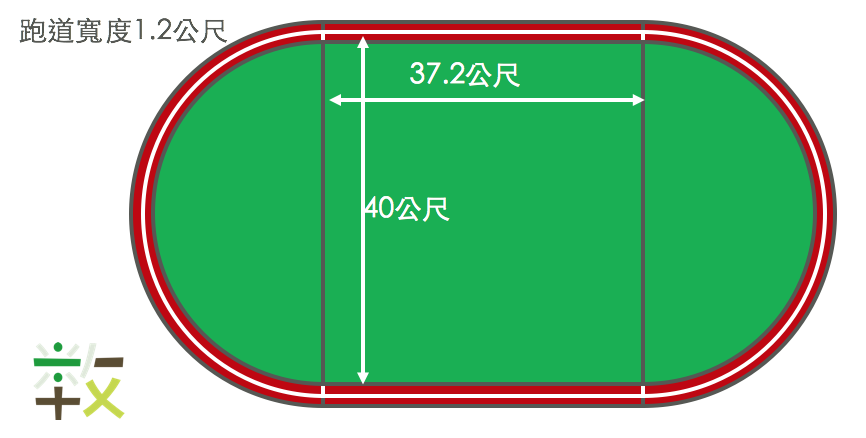
假設賽跑起點是直線跑道的起點,最佳的切內圈策略就是瞄準內圈在直線跑道盡頭的點前進,讓該點、直線跑道的內圈、以及自己此刻的位置三點形成一個直角三角形。這個直角三角形的底是37.2公尺,高是3.6公尺,斜邊是等等跑步的軌跡。
利用畢氏定理可以求出軌跡長度為(37.2的平方)+(3.6的平方),再開根號約是37.37公尺。換句話說,只要跑37.37公尺,不僅能跑完直線跑道,還能從外圈切到最內圈。比起沿著方才直角三角形底邊奔跑的內圈跑者來說,只僅僅多37.37-37.2=0.17,才多跑17公分!遠勝過「進入第二圈後轉90度直接往內圈衝刺」這個跑法。
差距是多少呢?以大隊接力為例,假如平均速度是100公尺15秒,則多跑17公分約是0.03秒的差距,幾乎可以忽略。但轉90度,依序沿著高跟底邊奔跑的跑法,多跑3.2公尺約是0.48秒的差距,這還沒算上距離增加,跑速會往下降的問題。
如果是更外線的跑道,或更大圈的賽道,差距會再增加,我們當然不可能採取「轉九十度」的奔跑策略,但也不是每個人都知道要在直線的最後一刻才能切入內圈,特別是當教練對你耳提面命「要盡快切入內圈」的時候。對賽跑來說,一毫秒的差距可能都是勝負的關鍵。想在賽場上獲勝,不僅需要認真的訓練,數學思維也是不可或缺的一部份。

沒有留言:
張貼留言